FlexPDE - 有限元计算软件

FlexPDE是基于有限元方法的偏微分方程（Partial Differential Equations,PDE）求解软件。新版本为Version 8。

FlexPDE软件由于其易学，比较人性化的计算流程，目前已被广泛应用。FlexPDE的主要功能有：可以求解一维到三维的问题；可以自动生成有限元网格；可以求解发展问题和稳态问题，以及特征值问题；支持可视化的计算结果显示；支持动网格等。,FlexPDE可获得偏微分方程的数值解，偏微分方程在工程上常见于，物理、电机、电子、通讯、土木、机械、化工、化学、生物学、地质学、数学和其他科学领域FlexPDE使用这超强有限元素方法获得数值解。然而，使用FlexPDE并不需要了解复杂的有限元素方法。

从应力分析到化学反应动力学再到股票期权定价，现在系统的数学建模以偏微分方程为主。FlexPDE通过处理方程式而不是应用程序来解决这些领域的数学基础。

FlexPDE是一个独立的处理系统：

• 分析您的问题描述

• 象征性的形成Galerkin有限元积分，导数和依赖项

• 建立耦合矩阵并求解

• 绘制结果

FlexPDE特征：  

• 自然的易学语言 

• 三维模型建立  

• 在偏微分方程系统中输入文字、添加问题描述、及时把问题具体成有限元模型； 

• 自动的网格结构； 

• 无限的方程集合体； 

• 联立方程不限数量； 

• 非线性方程求解； 

• 1D，2D和3D； 

• 时间相关、稳态和特征值； 

• 动态的时间步控制； 

• 动态的网格改良； 

• 任意的拉格朗日/欧拉移动网格； 

• 整合图片并输出； 

• 输入到TecPlot或Vislt进行可视化； 

• 可跨平台

FlexPDE可以在一维，二维或三维笛卡尔几何中，在一维球面或圆柱几何中，或在轴对称二维几何中求解一阶或二阶偏微分方程的系统，FlexPDE将转换传递给其他软件包进行处理。实际上，FlexPDE被设计成其他应用程序要求处理的软件包。能够键入偏微分方程系统，添加问题域的描述，并立即将此问题规范转换为复杂的有限元模型，包括:

•  一个，两个或三个空间维度

• 自动网格结构

• 时间相关，稳态或特征值

• 集成图片输出

动态自适应网格细化：

FlexPDE持续监控解决方案的准确性，并调整有限元网格以解决那些高误差区域。整个域中不需要密集网格，因为FlexPDE会找到需要它的区域，并将其放在那里。FlexPDE使网格适应波浪的前端。

• 动态时间步控制

• 非线性方程求解器

• 无限的方程复杂性

• 无限数量的联立方程

• 多个方程组

• 复杂，矢量和数组变量和方程

• 区域非活动变量

任意拉格朗日/欧拉移动网格：

FlexPDE允许定义网格移动方程，并应用任意拉格朗日/欧拉（ALE）公式。这允许几个可选行为：

• 通过将网格锁定到流体速度，您可以创建拉格朗日模型。

• 或者，您可以在移动边界内定义松弛网格以保持网格。

• 或者，通过省略网格移动方程，您可以执行欧拉计算。

• 在相关情况下，FlexPDE都会自动更正PDE系统以表示网格的运动。

第三方可视化的导出功能：

• 将FlexPDE数据导出到TecPlot或VisIt以获得令人惊叹的可视化效果

• 多核支持处理器

• CAD表面网格导入设施

FlexPDE 7功能：

1. Heirarchical Basis—新的heirarchical FEM基础函数改进了矩阵调节。

2. 内置参数optimizer

3. CAD网格导入—导入以CAD程序（OBJ） 格式创建的边界网格。

4. 一般边界形状—使用隐式代数方程创建边界路径。

5. 交互式绘图缩放—放大绘图而无需请求绘图。

6. 材料集—用户定义的材料属性组简化了脚本编写。

7. 边界条件集-用户定义的边界条件组简化了脚本缩写。

8. 多向周期性—支持角上多个方向的周期性边界。

9. 扩展选项面板—位于方便的选项面板中的主要位置。

10. 自动网格输出—使用自动网格传输输出更方便地进行后处理。

11. 自动网格输入—尽可能通过导入先前网格来更快地重新启动。

12. 简化停止和重新启动—用于从网格传输文件重新启动的简化命令。

13. 新的Dongle供应商—Wibu-Syatems加密狗提供更大的灵便性和成本效益。

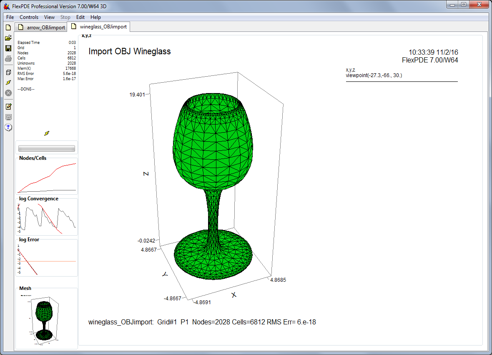
版本7—CAD导入的屏幕截图：

操作系统：

Windows 64（XP/Vista/7/8/10）（AMD64或Intel64）

Linux86 64（AMD64或Intel64）（在Suse Leap 42.2上编译）

MacOS （10.8至11.2）